PILCO: a model-based data efficient policy search algorithm

Content

1. Introduction
2. Explanation
3. Implementation Details
4. Comments

Introduction

Modern RL often suffers from data inefficieny. For example, have a look at a recent paper of openAI [1]. They require no more than several mounth of training with 32 NVIDIA V100 GPUs ( ~8000 £/ unit) and 400 workers with 32 CPU cores each. In the overall, it corresponds to roughly 13 thousand years of experience. Despite the impressive result on solving a Rubik’s cube using one dexterous robotic hand, the hardware and time requirements are unsitable for real world robotic applications.

One approach that still uses the RL paradigm is model-based RL. In this scenario, the agent can uses a model of the dynamics, i.e, how a given action \(u_t\) changes the state \(x_t\) of the system. Once this model is known, the agent can use it to find an policy. In other words, the model is a function \(\phi : \mathbf{S} \times \mathbf{A} \rightarrow \mathbf{S}\) where \(\mathbf{S} \in \mathbb{R}^N\) is the state space and \(\mathbf{A} \in \mathbb{R}^M\) is the action space. The issue however is that learning this model is a complex task. First, the data exploited to learn the model is noisy. Therefore, the model is only able to reach an approximation of the true dynamics. The second issue is known as model-bias. An illustration of model bias is shown in Figure [1]. Prediction from the model outside the training set are essentialy arbitrary but claimed with a high confidence.

Model-bias illustration.
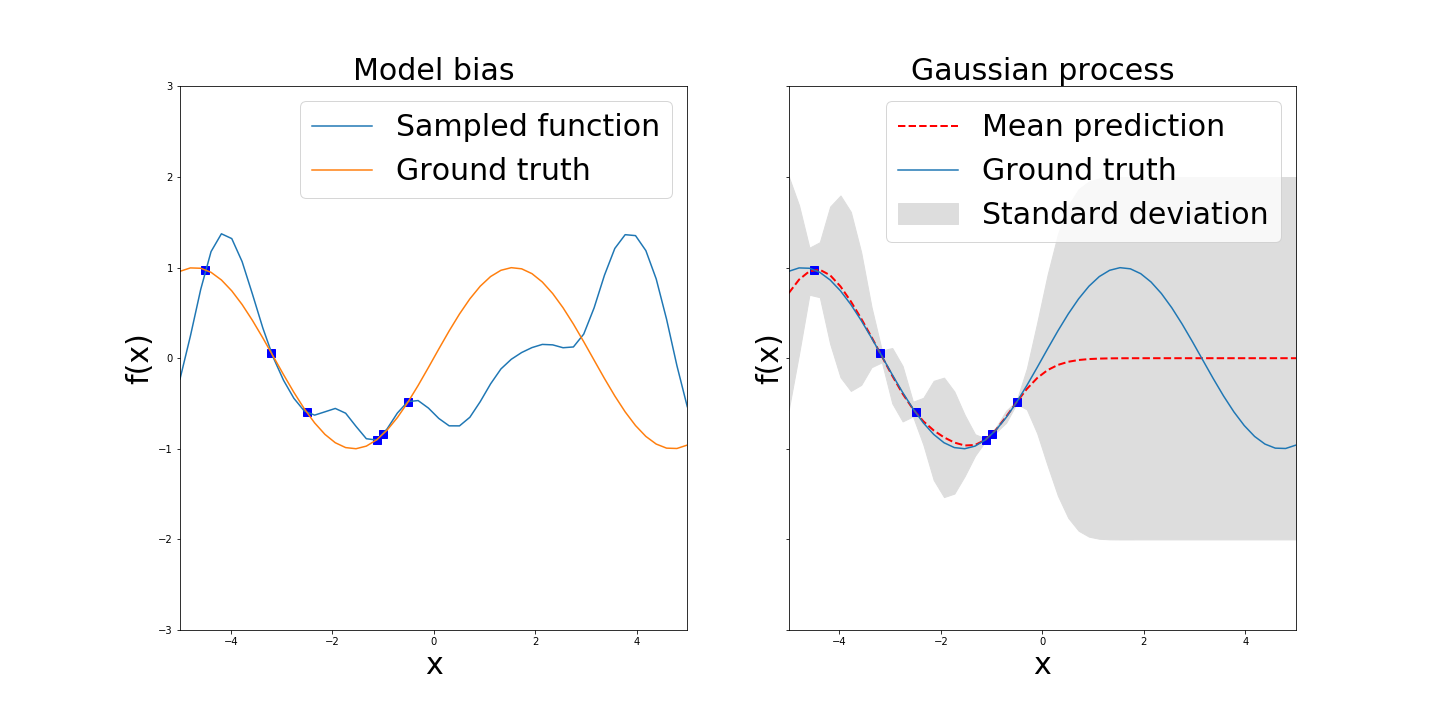
Leftmost: function matching the data but making overconfident predictions.
Rightmost: Gaussian process with mean and standard deviation

This can lead to unpredictable behaviors when the agents is in unexplored regions. In real world application with sparce datasets, this behavior is undesirable. On the other hand, one could model the dynamics of the system with a probabilistic model. [M. P. Deisenroth & al.] use Gaussian Processes (GPs) for this purpose. If you are unfamiliar with GPs, I suggest to read Katherine Bailey’s post about them. There main advantage is their ability to model the uncertainty about the prediction. Using this uncertainty into the policy planning process yields to PILCO, a data efficient policy search algorithm. Now we will explain this paper more in detail (beware, math are comming).

---

Explanations

Lets recall the objective. [M. P. Deisenroth & al.] considers the following transition dynamics function of the system: \[ x_{t+1} = \phi(x_t, u_t) \] Where \(x \in \mathbf{S}\) and \(u \in \mathbf{A}\). The goal is to find a deterministic policiy \(\mathit{\pi} : \mathbf{S} \rightarrow \mathbf{A}\) that minimizes the expected cost \[ J^{\pi_{\theta}}(x_0) = \sum_{t=0}^{T} \mathbb{E}_{x_t} [c(x_t)], \quad x_0 \sim \mathcal{N}(\mu_0, \Sigma_0) \]

where \(x_{t+1}\) is given by :

\[ x_{t+1} = \hat{\phi}(x_t, \pi{x_t}) \]

\(\hat{\phi}\) is the transition function learned by the agent.

Learning the Transition Function

First things first, we need to learn the probabilistic transition function presented earlier. The learning set is composed of \((x_{t}, u_{t}) \in \mathbf{S} \times \mathbf{A}\), used as input, and \(\Delta_{t+1} = x_{t+1} - x_{t} + \epsilon \in \mathbf{S}, \quad \epsilon \sim \mathcal{N}(0, \Sigma_{\epsilon})\)

Note: For those of you familiar with the RL litterature, the authors used a minimization of a cost function rather than a maximisation of a reward function.

Implementation Details

Comments

After running a couple of experiments, cart pole, double cart pole and double pendulum, here are my impression.

1. The learning time is quite long ~2h for the double cart pole. It is obviously less than for deep nn but the algorithm barely finds a solution to the problem. 10 trials ~ 20s of interaction. They extend this to 30 trials in the paper ~60s of interaction but this means more than 6h of optimisation as the number of training samples increase and GP are \(O(n^3)\) for the prediction step where n is the number of training samples.
2. Gradient descent on non-convex function is probably the main reasons for the poor solution. See figure 1.
3. It feels like the Gaussian process struggles at learning the dynamics of the system mostly for high dimensonal systems. The uncertainty propagation after multiple rollouts given the policy is still extremely uncertain. See figure 2.
4. Could reduce the learning time by throwing more computational power but this isn’t a viable solution for real robot applications.
5. I’m fairly certain that this algorithm will behave poorly on an AUV but I think that model-based RL with probabilistic model is a interesting path to follow. Main argument being that Model-Based rl are generally more data efficient (cite correct paper.) and optimisation under uncertainty seems to be intuitively more interesting, especially as mean models tend to make overconfident prediction in regions where there is no training sample which can be harmful for the agent or lead to suboptimal behaviors.
6. More recent method make use of BNN or NN ensemble to estimate the uncertainty of the prediction.

Sources

[1] OpenAI et al., “Solving Rubik\u2019s Cube with a Robot Hand,\u201d arXiv Prepr., 2019.

[2] M. P. Deisenroth and C. E. Rasmussen, “PILCO: A model-based and data-efficient approach to policy search,” Proc. 28th Int. Conf. Mach. Learn. ICML 2011, pp. 465–472, 2011.